Programmbeispiele
Sie können die Programme entweder per Mausklick ansehen oder (über das Menü der rechten Maustaste) dierekt herunterladen und abspeichern. Die Programmbeispiele sollen für den Leser eine Anregung zu weiteren Studien sein und können keinen Text oder Kurs über numerische Methoden in der Mathematik (wie etwa [ToSp88]}) ersetzen. Einen ausgezeichneten Überblick zu diesem Thema findet man in [PrFlTe99], wo auch eine entsprechende Programmbibliothek in allen gängigen Programmiersprachen vorgestellt wird.
Die Programmbeispiele sollen für den Leser ein Anregung zu weiteren Studien sein und können keinen Text oder Kurs über numerische Methoden in der Mathematik (wie etwa [ToSp88]) ersetzen. Einen ausgezeichneten Überblick zu diesem Thema findet man in [PrFlTe99], wo auch eine entsprechende Programmbibliothek aufgebaut wird.
Folgen
Das erste Beispiel ist ein Programm, um die Konvergenz oder Divergenz einer
Folge zu demonstrieren. Andere Folgen können durch entsprechende Änderung
der Funktion fg(n) untersucht werden.
FORTRAN90 Programm folgen.f90
Im zweiten Beispiel wird die logistische Abbildung untersucht, eine
Folge, die abhängig von einem Kontrollparameter konvergent oder auf
verschiedene Arten divergent ist.
FORTRAN90 Programm logmap.f90
Konvergenz von Partialsummen
Konvergenz von Potenzreihen
Hier wird der Wert der Partialsumme 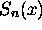 für einen Bereich in x mit einer gegebenen Funktion verglichen.
Die Konvergenzeigenschaften können durch Untersuchung verschiedener
Werte für n und x untersucht werden. Im Programmbeispiel
wird die Reihe für die Funktion cos x mit der Funktion selbst
verglichen. Man beachte die iterative Berechnung der Folgenglieder in der
Partialsumme!
für einen Bereich in x mit einer gegebenen Funktion verglichen.
Die Konvergenzeigenschaften können durch Untersuchung verschiedener
Werte für n und x untersucht werden. Im Programmbeispiel
wird die Reihe für die Funktion cos x mit der Funktion selbst
verglichen. Man beachte die iterative Berechnung der Folgenglieder in der
Partialsumme!
FORTRAN90 Programm partsum.f90
Potenzreihen - algebraisch
Hier ist eine Kollektion von Unterprogrammen, die Berechnung und Manipulationen
von Potenzreihen erlauben. Die Potenzreihen 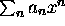 werden durch die Koeffizienten
werden durch die Koeffizienten 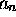 dargestellt. Die Programme zeigen die wesentlichen Strukturen und sollten
zu eigenen Erweiterungen (etwa für andere Winkelfunktionen oder den
natürlichen Logarithmus) anregen.
dargestellt. Die Programme zeigen die wesentlichen Strukturen und sollten
zu eigenen Erweiterungen (etwa für andere Winkelfunktionen oder den
natürlichen Logarithmus) anregen.
FORTRAN90 Programm polynome.f90
Numerische Interpolation
Die wenigen Testdaten in diesem Programmbeispiel zur numerischen Interpolation
sollten von Ihnen geeignet vermehrt werden. Sie befinden sich beim DATA-Befehl
in Paaren der Form 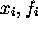 .
.
FORTRAN90 Programm intpol.f90
Fraktale
In diesem Programmbeispiel werden beliebige Ausschnitte der Mandelbrot-Menge
berechnet. Da die Rechnung zeitaufwendig ist, wird im Beispielsprogramm nur ein Feld von 200x200
Punkten dargestellt.
FORTRAN90 Programm mandel.f90
Doppelspalt-Beugungsbild
In diesem MATHEMATICA Programm wird die Intensitätsverteilung
des Beugungsbildes eines Doppelspalts berechnet und dargestellt.
MATHEMATICA Programm doppelspalt.m
Nullstellen von Funktionen
Es werden zwei Verfahren zur numerischen Bestimmung der Nullstelle
einer gegebenen Funktion in Programmbeispielen gezeigt: die Regula Falsi
und das Newtonsche Verfahren. In beiden Fällen muß ein Intervall
angegeben werden, in dem die Funktion einen Vorzeichenwechsel hat.
FORTRAN90 Programm regfalsi.f90
Das Newtonsche Verfahren kann in manchen Fällen aus dem vorgegebenen
Intervall hinauslaufen. In diesem Fall wird eine Fehlermeldung ausgeschrieben,
und es werden neue Intervallgrenzen angefordert. Dies kann insbesondere
dann passieren, wenn es im Intervall Punkte mit sehr kleiner 1. Ableitung
gibt. Oft hilft dann ein genaueres Einschränken des Intervalls.
FORTRAN90 Programm newton.f90
Numerische Differentiation
Äquipotentiallinien
Die Darstellung von Kurven konstanten Potentials oder konstanter Temperatur
ist ein nützliches Hilfsmittel zur Visualisierung.
FORTRAN90 Programm kontur.f90
Numerische Integration
In diesem Programmbeispiel werden sukzessive immer mehr Stützstellen zur
Abschätzung des Integrals herangezogen. Mit jedem Schritt verdoppelt sich
die Zahl der Stützstellen (und die benötigte Computerzeit). Obwohl
das Verfahren der erweiterten Trapezregel folgt, kann man das Ergebnis entsprechend
der erweiterten Simpsonregel durch Kombination von zwei aufeinanderfolgenden
Schätzwerten erhalten[PrFlTe99].
FORTRAN90 Programm trapint.f90
Monte Carlo Integration
Lösung eines Gleichungssystems
Statt den Gauß Algorithmus zu programmieren, verwenden wir die
in MATHEMATICA eingebauten Prozeduren, um ein Gleichungssystem zu lösen.
Im Prinzip kann man auch mit Matrizen arbeiten, deren Elemente nicht rein
numerisch angegeben sind, sondern Funktionen und Parameter enthalten.
MATHEMATICA Programm gauss.m
Methode der kleinsten Fehlerquadrate
Das Ausgleichsverfahren verwendet Polynome, aber man kann das Programm leicht
auf andere Funktionen umstellen. Wir zeigen zuerst etwas ausführlicher,
wie das Least Square Verfahren arbeitet. Am Ende verwenden wir die vorgesehene
Prozedur Fit.
MATHEMATICA Programm lsq.m
Computeranimation
Eine gegebene Menge von Strecken wird schrittweise im Raum gedreht
und auf dem Bildschirm dargestellt. Die Drehung und die Blickrichtung des
Beobachters können frei gewählt werden. Zur Unterstützung
der räumlichen Vorstellung wird auch ein raumfestes Koordinatensystem
gezeichnet.
FOTRAN90 Programm rotate.f90
Richtungsfeld
MATHEMATICA Programm zur graphischen Darstellung des durch eine lineare
DG gegebenen Richtungsfeldes.
MATHEMATICA Programm vecfld.m
Planetenbahnen
Dieses FORTRAN90 Programm löst die Gleichungen für ein Zentralkraftproblem,
wie es die Bewegung der Erde um die Sonne darstellt. Man kann das Programm
leicht auf mehrere Planeten und Monde erweitern. Die Kraft zwischen den
beiden Massenpunkten, die sich in einer Ebene bewegen, ist durch  gegeben. Bei mehreren Massepunkten setzt sich jede Kraft, die auf den jeweilig
betrachteten Massenpunkt wirkt, aus den Teilkräften zusammen.
gegeben. Bei mehreren Massepunkten setzt sich jede Kraft, die auf den jeweilig
betrachteten Massenpunkt wirkt, aus den Teilkräften zusammen.
FORTRAN90 Programm planet.f90
Relaxation
MATHEMATICA Programm zur Relaxation: Die Potentialwerte sind auf einem 50x50
Grid zu berechnen Die Randbedingungen (hier der äußere Rand und
die Werte an der Stelle der Punktladungen des Ladungspaars) werden durch das
Array ZRB festgelegt, die Randwerte und Anfangswert werden geeignet
initialisiert. Nach 100 Relaxationsschritten wird das Ergebnis graphisch dargestellt.
MATHEMATICA Programm relax.m
Schwingende Saite
MATHEMATICA Programm zur graphischen Darstellung einer
schwingenden Saite.
MATHEMATICA Programm saite.m
Schwingende kreisförmige Membran (Trommel)
MATHEMATICA Programm zur graphischen Darstellung von
Eigenschwingungen einer kreisförmigen Membran (Trommel)
mit Animation.
MATHEMATICA Programm drum.m
Allgemeine Relativitätstheorie
MATHEMATICA Programm zur Berechnung der Raumkrümmung im Rahmen
der Allgemeinen Relativitätstheorie.
MATHEMATICA Programm art.m
Literaturhinweise
- PrFlTe99
- W.H. Press, B.P. Flannery, S.A. Teukolsky und W.T. Vetterling, Numerical
Recipes (Cambridge University Press, Cambridge: 1999)
-
ToSp88
-
W. Törnig und P. Spelluci, Numerische Mathematik für Ingenieure
und Physiker, Band 1 und 2 (Springer-Verlag, Berlin: 1988)
➜ Zurück zu Programme


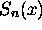 für einen Bereich in x mit einer gegebenen Funktion verglichen.
Die Konvergenzeigenschaften können durch Untersuchung verschiedener
Werte für n und x untersucht werden. Im Programmbeispiel
wird die Reihe für die Funktion cos x mit der Funktion selbst
verglichen. Man beachte die iterative Berechnung der Folgenglieder in der
Partialsumme!
für einen Bereich in x mit einer gegebenen Funktion verglichen.
Die Konvergenzeigenschaften können durch Untersuchung verschiedener
Werte für n und x untersucht werden. Im Programmbeispiel
wird die Reihe für die Funktion cos x mit der Funktion selbst
verglichen. Man beachte die iterative Berechnung der Folgenglieder in der
Partialsumme!
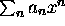 werden durch die Koeffizienten
werden durch die Koeffizienten 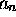 dargestellt. Die Programme zeigen die wesentlichen Strukturen und sollten
zu eigenen Erweiterungen (etwa für andere Winkelfunktionen oder den
natürlichen Logarithmus) anregen.
dargestellt. Die Programme zeigen die wesentlichen Strukturen und sollten
zu eigenen Erweiterungen (etwa für andere Winkelfunktionen oder den
natürlichen Logarithmus) anregen.
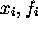 .
.
 gegeben. Bei mehreren Massepunkten setzt sich jede Kraft, die auf den jeweilig
betrachteten Massenpunkt wirkt, aus den Teilkräften zusammen.
gegeben. Bei mehreren Massepunkten setzt sich jede Kraft, die auf den jeweilig
betrachteten Massenpunkt wirkt, aus den Teilkräften zusammen.